Albert Einstein is attributed to having called compound interest “the eighth wonder of the world.”
And Benjamin Franklin famously ran a 200-year experiment to prove the power of compound interest, endowing 1,000 British pounds to Boston and Philadelphia. After nearly 200 years, both investments are now worth millions of dollars.
But what is compound interest, and how exactly does it work?
Simply put, compound interest is the process of your money making money, and then that money making even MORE money.
Let’s discuss how to calculate compound interest, how the effects of time make it so powerful, and how to use compound interest to plan your investments.
What is compound interest?
Compound interest refers to the process of earning interest on the principal amount of an investment, and the interest earned on the accumulated interest of that investment.
In other words, the interest you earn, in turn, also earns interest. The compounding interest allows your original investment to grow and earn more each year.
Compound interest is the foundation of growing your wealth, as you can earn more and more each year you stay invested. But it also works in reverse, as bank loans and credit cards also compound your debt interest, making you pay more and more over time.
Here’s a quick example:
If you invest $10,000 in a savings account earning a 5% annual interest rate, you will earn $500 in that first year. But in year two, you will earn the same $500 plus 5% interest on the $500 you earned the previous year, netting you $525 in year two. This continues each year of your investment, adding the earnings to your balance, and earning more and more interest as you stay invested.
Read more: Best high-yield savings accounts
How does compound interest work?
Compounding interest consists of:
- an investment amount (or debt amount)
- an interest rate
- a time period
- the compounding period
In the case of an investment, the principal balance earns interest that is paid out on a recurring basis (daily, monthly, annually, etc.), and added back to the principal balance.
Then, during the next cycle, you earn interest on both the principal investment AND the interest paid, compounding your returns.
The power of compounding is the frequency at which you earn interest, and the amount of time you allow the investment to grow. This can lead to exponential returns, earning more money each year, even if you don’t put any more money into the investment.
Read more: Essential advice to help you start investing
How is compound interest calculated?
To calculate compound interest your multiply the principal amount by one, plus the annual interest rate, to the power of the number of compounding periods, minus one.
Wait, what?
Here it is in formula form:
= P[(1+IR)N-1]
- P = principal amount
- IR = interest rate
- N = number of compounding periods
Still not any easier?
OK, here’s an example;
If you invest $1,000 over a 5-year period at 5% interest, here’s how much you’ll end up with:
$1,000[(1+0.05)5-1] = $1,000[1.27628] = $1,276.28
Got it?
OK, here’s a shortcut: just use our compound interest calculator instead.
How compounding frequency works
Compound interest is typically calculated on an annual basis, but the more frequent the compounding frequency, the higher the amount of interest you’ll earn on your investment.
For example, if your investment or savings account compounds monthly, you will add interest each month. So, if you deposit $10,000 at a 5% interest rate that compounded monthly, here’s how it compares to annual compounding:
- $10,000 invested compounding monthly for 5 years = $12,762.82
- $10,000 invested compounding annually for 5 years = $12,833.59
While the difference may seem small, you just earned another $70 without doing anything. And if the compounding frequency was daily, you would earn nearly $80 more interest.
For that reason, you should always favor interest-bearing investments that compound with the greatest frequency. Daily is typically the best option, while annually will provide the lowest return.
Compound interest and time
The most important factor that makes compound interest a powerful investing concept is time. The longer your investment is left alone to compound, the higher returns.
Like, exponentially higher!
Let’s take a look at compounding over a longer-term period of time.
You have three investments: Investment A, Investment B, and Investment C. The terms of each are as follows:
- Investment A: $10,000 invested at 5% for 10 years, compounded yearly
- Investment B: $10,000 invested at 5% for 20 years, compounded yearly
- Investment C: $10,000 invested at 5% for 30 years, compounded yearly
At the end of each term, here’s what the investments look like (and yes, I used the calculator for these results):
- Investment A: $16,288.95, comprising $10,000 in original principal, and $6,288.95 in interest earned over 10 years
- Investment B: $26,532.98, comprising $10,000 in original principal, and $16,532.98 in interest earned over 20 years
- Investment C: $43,219.42, comprising $10,000 in original principal, and $33,219.42 in interest earned over 30 years
As you can see from this example, Investment B didn’t earn double the amount of interest over the next 10 years, but almost triple! And Investment C earned almost 5x the interest as investment A, though only being invested for 3x the time.
The longer you stay invested, the more powerful compounding interest becomes.
Compound interest vs. simple interest
Some financial accounts pay simple interest instead of compound interest, which only pays interest on your initial investment. This is much worse for investors, but much better for debt arrangements.
Under a simple interest arrangement, you might invest $10,000 at a 5% rate of interest for one year. At the end of one year, you’ll receive $10,500 — $10,000 representing your original principal, plus $500 in interest earned. In year two, you’ll earn the same $500, and this will continue each year, without any additional interest added.
Compound interest adds the interest earned to your balance, allowing you to earn more each year. As illustrated earlier in this article, investing that same $10,000 at 5% interest will net you $500 in year one, $525 in year two, and more each subsequent year you are invested.
Overall, compound interest is far superior to simple interest for investments, but simple interest can save you money on loans and other debts. So you want compounding interest when you are investing and simple interest when you are borrowing.
Compound interest and the “Rule of 72”
This is a favorite rule of accountants, but it can also be a good tool for mere mortals. The Rule of 72 provides an approximation of how long it will take an investment to double in value based on a certain interest rate.
It works by dividing 72 by the rate of return on your investment.
For example, let’s say you invest $10,000 at 6%, and you want to know how long it will take to double your investment. By dividing 72 by 6%, you’ll get 12. That means it will take 12 years for the value of your investment to double at that annual percentage yeild.
The Rule of 72 won’t help you with more complicated calculations, but getting the answer to “when will my investment double” is a very common question among investors. And if you ever have that question with an investment you’re considering or already own, you can use the rule to find the answer for yourself.
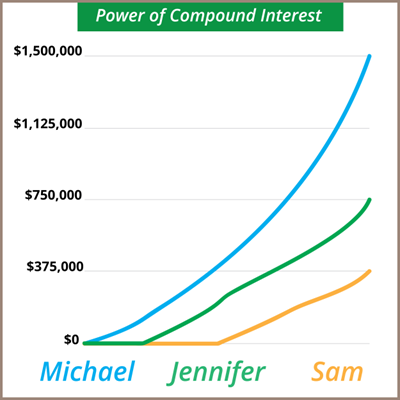
How investing early makes a difference (real-life example)
You may have heard that the earlier you start investing the better. Well, it’s true, and we’ve crunched the numbers to show you the difference your age can make when investing.
Michael, Jennifer, and Sam invested for 10 years, and, through an incredible stroke of investment luck, each earned the same average annual return (7%) consistently, until age 65. The only difference between these investors is the year when they start socking away their funds.
Michael saved $1,000 per month from the time he turned 25 until he turned 35. Then he stopped saving but left his money in his investment account, where it continued to accrue at a 7% rate until he retired at age 65.
Jennifer held off and didn’t start saving until age 35. She put away $1,000 per month from her 35th birthday until she turned 45. Like Michael, she left the balance in her investment account, where it continued to accrue at a rate of 7% until age 65.
Sam didn’t get around to investing until age 45. Still, he invested $1,000 per month for 10 years, halting his savings at age 55. Then he also left his money to accrue at a 7% rate until his 65th birthday.
Michael, Jennifer, and Sam each saved the same amount — $120,000 — over a 10-year period.
Sadly for Jennifer, and even more so for Sam, their ending balances were dramatically different.
- Michael: $1,444,969
- Jennifer: $734,549
- Sam: $373,407
How to use compound interest to your advantage
Compounding interest is one of your best friends on the investment side. But it’s also something of an enemy when you borrow money. That’s because it works the same in both directions, except that with an investment, you’re on the receiving side of the interest equation. With a loan, you’re on the paying side, which means the interest will cost you more.
There are ways to play compound interest when it comes to both investments and loans.
To use compound interest to your advantage with investments:
- Choose investments that have the most frequent compounding possible. Daily or continuously are the best choices.
- Invest as soon as possible. Compounding of interest works best over longer terms.
- Let “APY” be your guide. That’s annual percentage yield, which reflects the interest you’re earning including compound. It’s the best way to compare one interest-bearing investment with another.
To use compound interest to your advantage with loans:
- Pay close attention to your interest rate – That’s the annual percentage rate (APR) on a loan. It reflects not only compounding of interest paid to the lender, but also any fees that you may pay in connection with obtaining or maintaining a loan. In the lending industry, flat interest rates, like 17.99% don’t matter nearly as much as an APR of 19.12%. The latter is the effective rate you’re really paying.
- Keep your loan terms as short as possible. Just as compound interest works to your advantage over longer terms with investing, it works against you when it comes to borrowing.
- Make additional payments. Making additional principal payments won’t lower your APR, but it will reduce the amount of interest you’ll pay over the life of the loan, as well as the term of the loan.
Once you understand how the power of compound interest works, you can make it your friend whether you’re looking to invest or borrow money.
Summary
When you earn compound interest, you’re earning interest on your interest. And the earlier you start, the better. Giving compound interest more time will help you exponentially grow your investments.
But it also works in reverse, and compound interest can accrue on your debt and increase your balances over time, so finding a good debt payoff strategy can help you save a lot of money.
Featured image: eamesBot/Shutterstock.com


